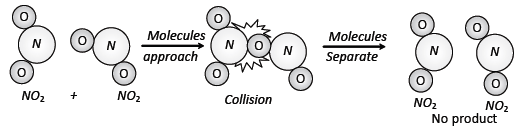
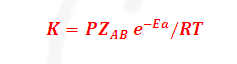The temperature dependence of rate of a chemical reaction
can be accurately explained by Arrhenius equation. It was first proposed by
Dutch chemist J.H. Vant’s Hoff but
Swedish chemist Arrhenius provides its physical justification and
interpretation.
Where K= Rate constant
A= Arrhenius constant or
frequency factor or pre exponential factor
R= Universal gas constant =25/3
joule per mole per second
Ea=
Activation Energy
T= temperature
-Ea/RT= Boltzmann factor or fraction of molecule having equal
or
greater than Activation energy or fraction of molecule that have kinetic energy
greater than activation energy.
ILLUSTRATIVE EXAMPLE (1): The activation energy for the reaction is 209.5 k J per mole
at 581 K.
Calculate
the faction of molecule of reactant s having energy equal to or greater than
activation energy.
SOLUTION: We known that fraction of molecule that have
kinetic energy greater than activation energy is given by
Important cases of
Arrhenius equation:
Case (1): If T approaches to infinite
It means the
entire reactant molecule will be active; and crossing over the energy barrier. It will be possible when either Ea is
Zero or temperature (T) is infinite. These are practically not
possible.
The maximum
value of K is A
when temperature tends to infinity.
Graph
indicate larger the activation energy, smaller is the value of rate constant
(K)
Note:
For free radical combination reaction (Ea=0 ) thus K=A ,that means for free radical reaction rate
constant equal to Arrhenius factor
and becomes independence of temperature .
Case (2): We know that (Ea) activation energy is always positive, thus
K always increasing with increasing temperature whether reaction is exothermic
or endothermic
Mathematical prove: since activation energy is always
positive it can be never negative this is proven as:
Case (3): However in many complex reactions it
is observed that rate constant found to be decreases with increasing
temperature.
For example
Mechanism:
By equation
(1) and (2)
Since the
overall reaction is exothermic and Kc
decreases with increasing
temperature as well as the decrease in Kc out
weight the increase in K with
temperature, thus K obs show
a decrease with increase in temperature.
Case (4): larger the activation energy greater the effect of
temperature on rate constant.
Case (5): At
lower temperature, increase in temperature causes more changes in value of rate
constant
Case (6):
“It means if
Ea=RT then rate constant become about 37% of the Arrhenius constant.
ILLUSTRATIVE EXAMPLE (2): Consider the following reaction
The
activation energy of backward reaction exceeds that of the forward reaction by
2RT (in J per mole). If the pre-exponential factor of forward reaction is 4
times of the reverse reaction. The absolute value of (G) Gibbs energy at STP
(in j per mole) for the reaction at 300 K is
(Given ln2= 0.7, RT= 2500 J per Mole at 300 K
and G is the Gibbs energy) (JEE Advanced 2018)
SOLUTION: Given condition
ILLUSTRATIVE EXAMPLE (3): Plots showing the variation of rate
constant (K) with temperature (T) are given below. The plot that follow
Arrhenius equation is (JEE Advanced 2010)
SOLUTION:
Hence on increasing
temperature rate constant (K) increases exponentially.
So option (A) is
correct
Calculation Activation Energy:
Take both side natural logarithm
and obtained as
Note:
(1): The above equation is the straight line
with negative slope
(2): The slope of above equation gives
Activation energy and intercept gives frequency factor
(3) Dependence of rate constant on
temperature for two reactions is given as:
Slope of
reaction (2) is greater than (1) hence reaction (2) has higher activation
energy so reaction (2) is more sensitive to temperature.
Calculation Activation Energy
at two different temperatures (T1 and T2):
ILLUSTRATIVE EXAMPLE (4): In Arrhenius equation for a certain
reaction, the value of A and Ea (activation energy) are 4 × 1013 sec–1 and 98.6
kJ mol–1 respectively. At what temperature, the reaction will have specific
rate constant 1.1 × 10–3 sec–1?
SOLUTION: According to Arrhenius
equation
ILLUSTRATIVE
EXAMPPLE (5): The energy of activation for a reaction is 100 kJ mol–1.
Presence of a catalyst lowers the energy of activation by 75%.What will be
effect on rate of reaction at 20ºC, other things being equal?
SOLUTION: The Arrhenius
equation is
Related Questions: