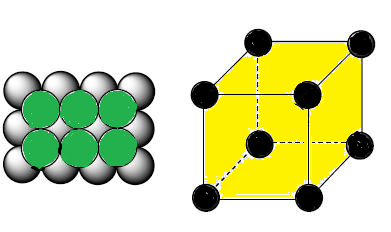
(1) A more efficiently packed cubic
structure is the "body-centered cubic" (bcc).
(2) The first layer of a square array is
expanded slightly in all directions. Then, the second layer is shifted so its
spheres nestle in the spaces of the first layer.
(3) This repeating order of the layers is often symbolized as
"ABA...".The considerable space shown between the spheres
is misleading: spheres are closely packed in bcc solids and touch along the
body diagonal.
(4) The packing efficiency of the bcc
structure is about 68%. The coordination number for an atom in the bcc
structure is eight.
(5)
Both SCC and BCC are not a closed packing
in 3D.
(6)
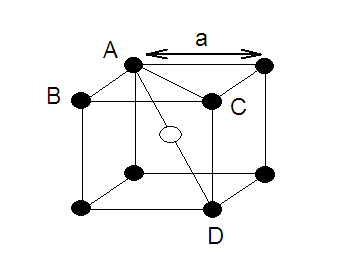
BCC crystal lattice is basically fusion of two simple unit cell in such that
coner of one simple unit cell become body centred atom of another simple unit
cell.
(7)
Radius of atom and Packing efficiency in BBC unit cell:
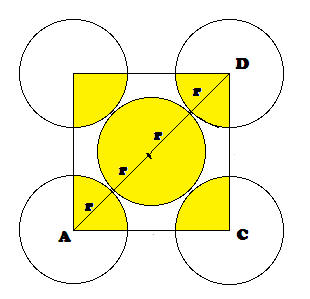
Consider ‘r’ is the radius of sphere and ‘a’ be the edge
length of the cube and the sphere at the centre touches the sphere at the
corner. Therefore body diagonal
Packing
efficiency (PE): Percentage of space occupied by spheres
No. of spheres in bcc = 2
Volume of 2 spheres = 2´4/3pr3
Empty
space (% Voids) = 100- 68= 32 %
(8) Density of BCC unit cell:
(9)
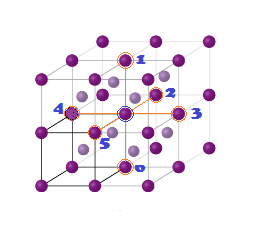
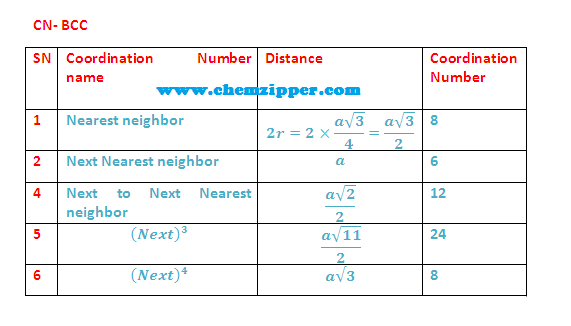
Coordination Numbers:
(1) The nearest neighbour distance is half of body
diagonal (a) root
3/2 (along body diagonal) therefore coordination number for a
given atom in BCC unit cell is 8.
(2)
The next nearest
neighbour are 6 at distance (a) Lattice parameter.
(3) 3rd neighbour (Next to Next nearest
neighbour) are (12)
at distance (a root 2) ( All corner along face diagonal in x,y
and Z plane).
ILLUSTRATIVE EXAMPLE (1): An element has a body-centred cubic (bcc) structure with a cell edge
of 288 pm. The density of the element is 7.2 g/cm3. How many atoms are present
in 208 g of the element ?
SOLUTION:
ILLUSTRATIVE EXAMPLE (1): How many 'nearest' and 'next nearest' neighbours respectively does
potassium have in b.c.c. lattice
SOLUTION: 8 and 6



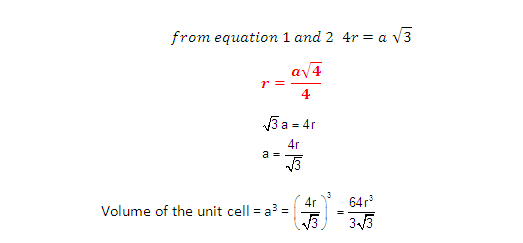

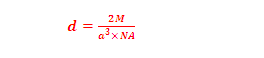



It was very helpful Thanks 😊😊
ReplyDeletethank you for comment
ReplyDeletesd
ReplyDeleteSuperb
ReplyDelete