FACE CENTRED UNIT CELL (FCC/CCP):

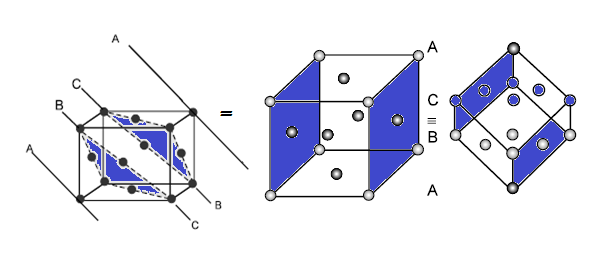
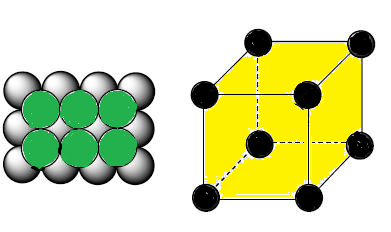
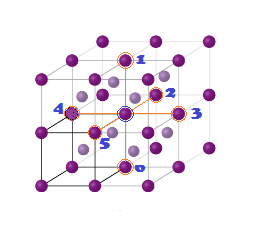
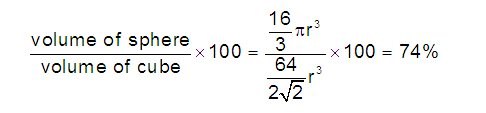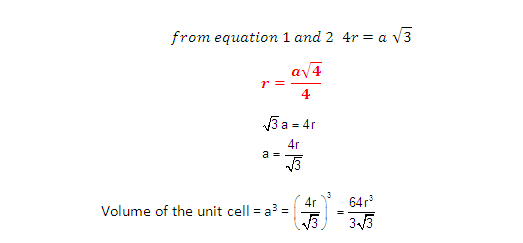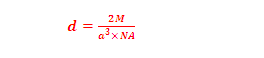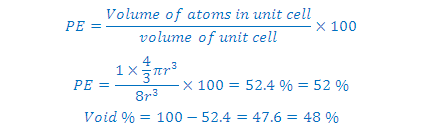CCP or FCC has two lattice point corner as well as face centred:

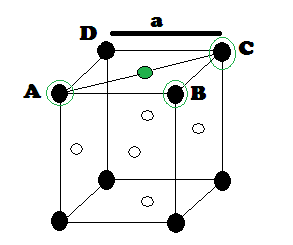
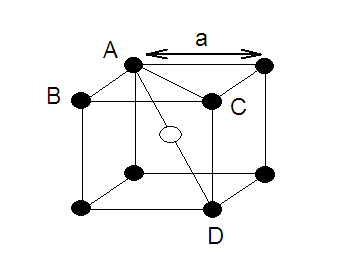
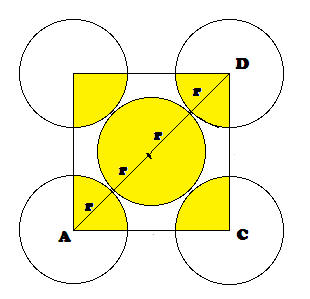
Suppose ‘r’ be the radius of sphere and ‘a’ be the edge length of the cube As there are 4 sphere in FCC unit cell

(1) Relation between radius (r) and side (a)

In FCC, the corner spheres are in touch with the face centred sphere. Therefore, face diagonal AD is equal to four times the radius of sphere AC = 4r

But from the right angled triangle ABC:

(2)  Effective no. of atoms per unit cell (Z):

(3) Volume of four spheres (atoms):

(4) Volume of unit cube:

(5) Packing efficiency (PE): Percentage of space occupied by sphere

(6) Percentage Voids: 100- PE= 26 %

(7) Density of FCC(CCP):

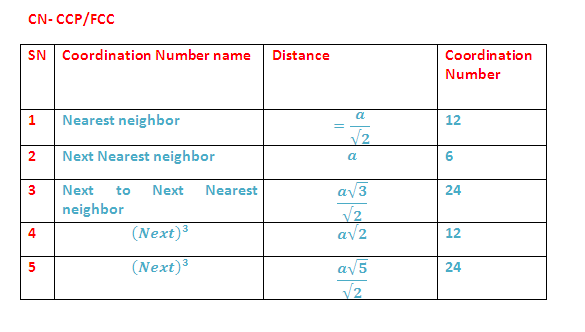
(8) Coordination Numbers:

(9) LOCATION OF VOIDS: FCC/CCP UNIT CELL:

(A) Tetrahedral voids: The FCC/CCP unit cell has eight tetrahedral voids per unit cell. Just below every corner of the unit cell, there is one tetrahedral void. As there are eight corners, there are eight tetrahedral voids.

(B) Octahedral voids: In an FCC/CCP unit cell, there are four octahedral voids. They are present at all the edge centres and at the body centre. The contribution of the edge centre is 1/4

Hence, total number of octahedral voids:

In CCP/FCC:

 Rank (Z) = 4,

 Number of tetrahedral voids = 8 and

 Number of tetrahedral voids = 2 × Z

Number of tetrahedral voids in close packing = 2 × eff. no. of spheres.

Hence, there are two Tetrahedral Voids per sphere in closed packing arrangements.

In CCP/FCC:

 Z = 4

Number of octahedral voids = 4 

Number of octahedral voids = Z

There is exactly one OV per sphere in close packing.

BODY CENTERED CUBIC CELL (BCC):

(1) A more efficiently packed cubic structure is the "body-centered cubic" (bcc).

(2) The first layer of a square array is expanded slightly in all directions. Then, the second layer is shifted so its spheres nestle in the spaces of the first layer.

(3) This repeating order of the layers is often symbolized as "ABA...".The considerable space shown between the spheres is misleading: spheres are closely packed in bcc solids and touch along the body diagonal.

(4) The packing efficiency of the bcc structure is about 68%. The coordination number for an atom in the bcc structure is eight.

(5) Both SCC and BCC are  not a closed packing in 3D.

(6) BCC crystal lattice is basically fusion of two simple unit cell in such that coner of one simple unit cell become body centred atom of another simple unit cell.

(7) Radius of atom and Packing efficiency in BBC unit cell:

Consider ‘r’ is  the radius of sphere and ‘a’ be the edge length of the cube and the sphere at the centre touches the sphere at the corner. Therefore body diagonal

Packing efficiency (PE): Percentage of space occupied by spheres

No. of spheres in bcc = 2

Volume of 2 spheres = 2´4/3pr³

Empty space (% Voids) = 100- 68= 32 %

(8)  Density of BCC unit cell:

(9) Coordination Numbers:

(1) The nearest neighbour distance is half of body diagonal (a) root 3/2 (along body diagonal) therefore coordination number for a given atom in BCC unit cell is 8.

(2) The next nearest neighbour are 6 at distance (a) Lattice parameter.

(3) 3^rd neighbour (Next to Next nearest neighbour) are (12) at distance (a root 2) ( All corner along face diagonal in x,y and Z plane).

ILLUSTRATIVE EXAMPLE (1): An element has a body-centred cubic (bcc) structure with a cell edge of 288 pm. The density of the element is 7.2 g/cm3. How many atoms are present in 208 g of the element ?

SOLUTION:

ILLUSTRATIVE EXAMPLE (1): How many 'nearest' and 'next nearest' neighbours respectively does potassium have in b.c.c. lattice

SOLUTION: 8 and 6

SIMPLE CUBIC CELL(SCC):

(1) 2D square close packing sheets are involved to generate simple cubic cell as well as body centred cell. In which each corner atom is touching potion with its adjacent corner atom.

(2) Take two 2D square close packing sheet and Placing a second square packing layer (sheet) directly over a first square packing layer forms a "simple cubic" structure.

(3) The simple “cube” appearance of the resulting unit cell is the basis for the name of this three dimensional structure.

(4) This packing arrangement is often symbolized as "AA...", the letters refer to the repeating order of the layers, starting with the bottom layer.

(5) The coordination number of each lattice point is six. This becomes apparent when inspecting part of an adjacent unit cell.

(6) The unit cell contain eight corner spheres, however, the total number of spheres within the unit cell is 1 (only 1/8th of each sphere is actually inside the unit cell). The remaining 7/8ths of each corner sphere resides in 7 adjacent unit cells.

(7) PACKING EFFICIENCY):

In simple cubic unit cell:

(1) Let ‘a’ be the edge length of the unit cell and r be the radius of sphere.

(2) As sphere are touching each other therefore a = 2r

(3) No. of spheres per unit cell = 8*1/8=1

(4) Volume of the sphere = 4/3(pi) r³

(5) Volume of the cube = a³= (2r)³ = 8r³

(6)  Packing efficiency (space occupied):

(7) Density of simple unit cell:

(8) Coordination Number:

(1) The nearest neighbour distance is just the lattice parameter (a) therefore coordination number for a given atom in SCC unit cell is 6 (six).

(2) The next nearest neighbour are 12 at distance a/root 2 (each face diagonal in x ,y and Z plane).

(3) 3^rd neighbour (Next to Next nearest neighbour) are (8) at distance a root 3 (each corner along body diagonal.