The
structure of crystalline solids is determined by packing of their constituents
.In order to
understand the packing of the constituent particles in a crystal;
it is assumed that these particles are
hard spheres of identical size (eg those
of metal). The packing of these spheres takes place in such a
way that they
occupy the maximum available space and hence the crystal has maximum density.
This
type of packing is called close packing.
TWO
DIMENSIONAL PACKING (2D):
When the
rows are combined touching each other, the crystal plane is obtained. The rows
can be combined in two different ways
(A) Square close packing:
(1) The particles when placed in the adjacent rows
show a horizontal as well as vertical (head to head) alignment and form
squares. This type of packing is called square close packing.
(2) Packing efficiency
calculation:
(1)
One sphere will be in constant contact with 4 other spheres hence coordination
number is 4
(2)
Side of Square is (a) and a=2r where r is the radius of atom (sphere).
(3)
Area of square = a2 = 4r2
(4) Area of atoms in the square is
(5) Packing fraction (PE) , fraction of area occupied by spheres
.
(B) Hexagonal close packing:
(1) The particles in every next row are placed in
the depressions between the particles of the first row. The particles in the
third row will be vertically aligned with those in the first row. This type of
packing gives a hexagonal pattern and is called hexagonal close packing
(2) Packing efficiency
calculation:
(1)
One sphere will be in constant contact with 6 other spheres hence coordination number
is 6
(2)
Side of hexagon is a and a=2r where r is the radius of atom (sphere) .
(3)
Area of hexagon unit cell is 6*area of six equilateral triangles
(4) Area of atoms in the hexagon unit
(5)
Packing fraction (PE) , fraction of area occupied by spheres
THREE DIMENSIONAL PACKING (3D):
(1) 3D SIMPLE CUBIC CELL AND BODY
CENTRED CELL (SCC AND BBC):
(A) Simple (primitive)
Cubic Cell (SCC) structure:
(1) 2D square close packing sheets are
involved to generate simple cubic cell as well as body centred cell. In which each corner atom is touching potion with its adjacent corner atom.
(2) Take two 2D square close packing
sheet and Placing a second square packing layer (sheet) directly over a first
square packing layer forms a "simple cubic" structure.
(3) The simple “cube” appearance of the
resulting unit cell is the basis for the name of this three dimensional
structure.
(4) This packing arrangement is often symbolized as
"AA...", the letters refer to the repeating order of the
layers, starting with the bottom layer.
(5) The coordination number of each
lattice point is six. This becomes apparent when inspecting part of an adjacent
unit cell.
(6) The unit cell contain eight corner spheres, however, the total number of
spheres within the unit cell is 1 (only 1/8th of each sphere is actually inside
the unit cell). The remaining 7/8ths of each corner sphere resides in 7
adjacent unit cells.
(7) PACKING EFFICIENCY AND COORDINATION NUMBER:
(7) PACKING EFFICIENCY AND COORDINATION NUMBER:
(2) Body Centered Cubic (bcc) Structure:
(1) A more
efficiently packed cubic structure is the "body-centered cubic"
(bcc).
(2) The first
layer of a square array is expanded slightly in all directions. Then, the
second layer is shifted so its spheres nestle in the spaces of the first layer.
(3) This repeating
order of the layers is often symbolized as "ABA...". Like
Figure 3b, the considerable space shown between the spheres in Figure 5b is
misleading: spheres are closely packed in bcc solids and touch along the body
diagonal.
(4) The packing
efficiency of the bcc structure is about 68%. The coordination number for an
atom in the bcc structure is eight.
(5) PACKING EFFICIENCY AND COORDINATION NUMBER:
THREE DIMENSIONAL CLOSED PACKING (3D):
(2) CUBIC CLOSE PACKING AND HEXAGONAL PACKING (CCP AND HCP)
THREE DIMENSIONAL CLOSED PACKING (3D):
(2) CUBIC CLOSE PACKING AND HEXAGONAL PACKING (CCP AND HCP)
Step-(1) In order to
develop three
dimensional close packing take a 2D hexagonal close packing sheet as
first layer (A- layer).
Step-(2) Another 2D hexagonal
close sheet (B-layer)
is taken and it is just over the depression (Pit) of the first layer (A) .When
the second layer is placed in such a way that its spheres find place in the ‘b’ voids
of the first layer, the ‘c’ voids will be left unoccupied. Since under
this arrangement no sphere can be placed in them, (c voids), i.e. only half (50%)
the triangular voids in the first layer are occupied by spheres of the second
layer (i.e. either b or c)
Step-(3) There are two
alternative ways in which spheres in the third layer can be arranged over the
second layer
(1) When
a third layer is placed over the second layer in such a way that the spheres
cover the tetrahedral
or ‘a’ voids; a three dimensional closest packing is obtained where
the spheres in every third or alternate layers are vertically aligned (i.e. the
third layer is directly above the first, the fourth above the second layer and
so on) calling the first layer A and second layer as layer B, the arrangement is
called ABAB …………. pattern
or hexagonal
close packing (HCP) as it has hexagonal symmetry.
(2) When
a third layer is placed over the second layer in such a way that spheres cover
the octahedral
or ‘c’ voids, a layer different from layers A and B is produced. Let
it be layer ‘C’. Continuing further a packing is obtained where the spheres in
every fourth layer will be vertically aligned to the spheres present in the
first layer. This pattern of stacking spheres is called
ABCABC ……….. pattern or cubic close packing (CCP). It is similar to face
centred cubic (fcc) packing as it has cubic symmetry
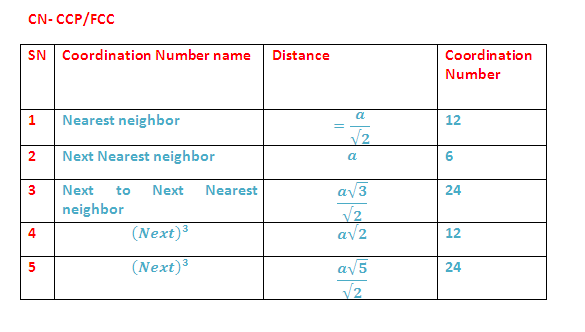
In both
HCP and CCP methods of stacking, a sphere is in contact with 6 other spheres in
its own
layer. It directly touches 3 spheres in the layer above and three
spheres in the layer below. Thus
sphere has 12 close neighbours.
The number of nearest neighbours in a packing is called coordination
number. In close packing arrangement (HCP & CCP) each sphere has
a coordination number of 12.
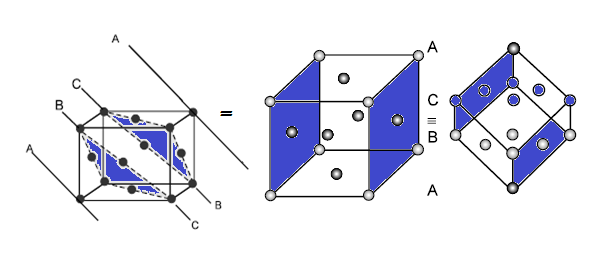
(3) FACE CENTRED UNIT CELL (FCC/CCP):
CCP or FCC has two lattice point corner as well as face centred:
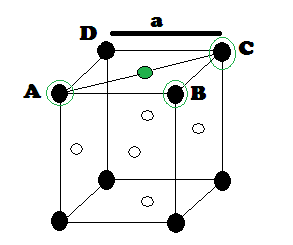
Suppose ‘r’ be the radius of sphere and ‘a’ be the edge length of the cube As there are 4 sphere in FCC unit cell
(1) Relation between radius (r) and side (a)
In FCC, the corner spheres are in touch with the face centred sphere. Therefore, face diagonal AD is equal to four times the radius of sphere AC = 4r
But from the right angled triangle ABC:
(2) Effective no. of atoms per unit cell (Z):
(3) Volume of four spheres (atoms):
(4) Volume of unit cube:
(5) Packing efficiency (PE): Percentage of space occupied by sphere
(6) Percentage Voids: 100- PE= 26 %
(7) Density of FCC(CCP):
(8) Coordination Numbers:
(9) LOCATION OF VOIDS: FCC/CCP UNIT CELL:
(A) Tetrahedral voids: The FCC/CCP unit cell has eight tetrahedral voids per unit cell. Just below every corner of the unit cell, there is one tetrahedral void. As there are eight corners, there are eight tetrahedral voids.
(B) Octahedral voids: In an FCC/CCP unit cell, there are four octahedral voids. They are present at all the edge centres and at the body centre. The contribution of the edge centre is 1/4
Hence, total number of octahedral voids:
In CCP/FCC:
Rank (Z) = 4,
Number of tetrahedral voids = 8 and
Number of tetrahedral voids = 2 × Z
Number of tetrahedral voids in close packing = 2 × eff. no. of spheres.
Hence, there are two Tetrahedral Voids per sphere in closed packing arrangements.
In CCP/FCC:
Z = 4
Number of octahedral voids = 4
Number of octahedral voids = Z
There is exactly one OV per sphere in close packing.
Step-(1) In order to develop three dimensional close packing take a 2D hexagonal close packing sheet as first layer (A- layer).
Step-(2) Another 2D hexagonal close sheet (B-layer) is taken and it is just over the depression (Pit) of the first layer (A) .When the second layer is placed in such a way that its spheres find place in the ‘b’ voids of the first layer, the ‘c’ voids will be left unoccupied. Since under this arrangement no sphere can be placed in them, (c voids), i.e. only half (50%) the triangular voids in the first layer are occupied by spheres of the second layer (i.e. either b or c)
Step-(3) There are two alternative ways in which spheres in the third layer can be arranged over the second layer
(1) When a third layer is placed over the second layer in such a way that the spheres cover the tetrahedral or ‘a’ voids; a three dimensional closest packing is obtained where the spheres in every third or alternate layers are vertically aligned (i.e. the third layer is directly above the first, the fourth above the second layer and so on) calling the first layer A and second layer as layer B, the arrangement is called ABAB …………. pattern or hexagonal close packing (HCP) as it has hexagonal symmetry.
ANALYSIS OF HCP UNIT CELL:
(1) Number of effective atoms in HCP unit cell (Z):
Lattice point: corner- total 12 carbon contribute 1/6 to the unit cell
Lattice point: face- total face 2 contribute ½
Lattice point: body centre- total atom 3 (100% contribution)
(2) Radius of atom in HCP unit cell:
Let the edge of hexagonal base =( a) And the height of hexagon =( h) And radius of sphere =( r)
(3) Area of hexagon:
Area of hexagonal can be divided into six equilateral triangles with side 2r
(4) Height of HCP unit cell:
(5) Volume of hexagon = area of base x height
(6) Volume of spheres:
(7) Packing efficiency: Percentage of space occupied by sphere.
(8) Voids %: 100 - PE= 26 %
(9) Coordination Numbers: 12 (each spheres touches 6 spheres in its layer,3 above and 3 below).
























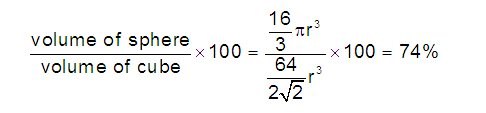
















Superb and clear explanation. Thank you so much
ReplyDeletethank a lot !!
Deletetq
Deletetq
DeleteCrystal clear explanation
ReplyDeletethank you for your comment !
Delete👍
ReplyDeletethank you very much !
DeleteI know the hardwork for making such blog , and therefore I truly appreciate your work, keep going 👍🏻
ReplyDelete😊😊
Deletethanks
ReplyDeleteGood explanation. It helps me lot
ReplyDeletethank you for your kind word , you can also easily understand by this unique model which is available on amazon you can by this link https://amzn.to/39kwz7f
DeleteThank you so much . God bless you
ReplyDeleteI Really Appreciate it
ReplyDeletethanks for comments
DeleteNice content !You were so dedicated for your work which inspired us alot. Thanks for being a great part of my learning experience.
ReplyDeleteThanks ChemZipper !! Helped me a lot to visualize
ReplyDeleteFinally I realise that platform is sufficient for me .thank u sir ❤️
ReplyDelete